

04/09/2023 (última actualización: 04/09/2023)
Infantil
Primaria
Matemáticas
Teoría
Orden
Ordinales
¡Hola, profesores y educadores! Hoy vamos a explorar un concepto matemático emocionante que es esencial para el desarrollo de las habilidades de conteo y ordenamiento: los números ordinales.
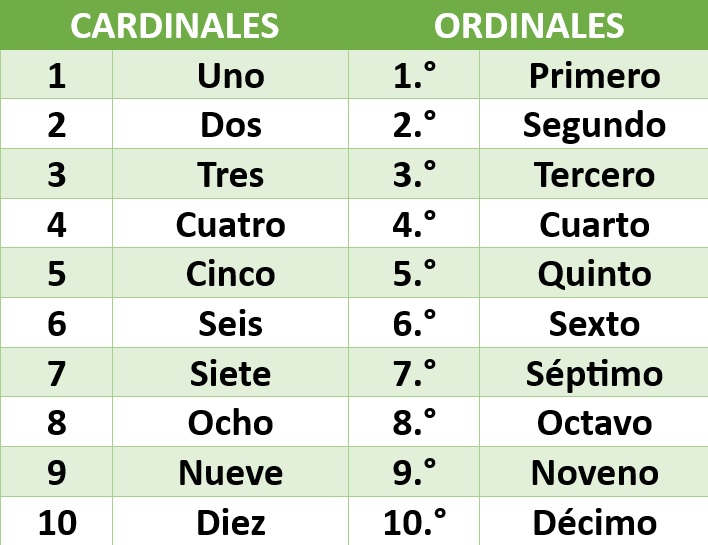
Los números ordinales son una forma especial de contar que se utiliza para indicar la posición o el orden de los elementos en una serie o conjunto. Mientras que los números cardinales, como 1, 2 y 3, se utilizan para contar la cantidad de objetos en un grupo, los números ordinales, como primero, segundo, tercero, se usan para describir el lugar o posición de un objeto en una secuencia.
El aprendizaje de los números ordinales se basa en varios principios matemáticos fundamentales, algunos de los cuáles ya hemos tratado en este blog, que ayudan a los estudiantes a comprender el concepto de posición y orden en una secuencia.
Los números ordinales implican ordenar elementos en una secuencia. Este principio matemático fundamental se refiere a la capacidad de colocar objetos o elementos en una fila o lista de manera organizada, de modo que cada uno tenga un lugar único y específico. Es decir, el principio del ordenamiento es un concepto matemático fundamental que subyace en la comprensión y aplicación de los números ordinales. Implica la capacidad de organizar objetos o elementos en una secuencia de manera lógica y estructurada. Este principio permite asignar a cada elemento de la secuencia un lugar único y específico, identificando así su posición relativa con respecto a los demás elementos.
El ordenamiento se aplica a una secuencia de elementos, lo que significa que estos elementos se disponen en un orden particular. La secuencia puede ser ascendente (de menor a mayor) o descendente (de mayor a menor), y los números ordinales se utilizan para etiquetar cada elemento en esa secuencia.
Cada elemento en la secuencia tiene una posición única y específica. Esta posición está determinada por su número ordinal correspondiente. No puede haber duplicados ni elementos que compartan la misma posición.
El ordenamiento permite comparar las posiciones relativas de los elementos en la secuencia. Por ejemplo, si se tienen tres elementos en una secuencia, el primero (primero) se encuentra antes que el segundo (segundo) y el tercer elemento (tercero).
El ordenamiento no se limita a secuencias numéricas simples. Puede aplicarse a una variedad de contextos, como clasificar objetos por tamaño, organizar eventos en un calendario, o determinar la clasificación de competidores en una carrera.
El principio del ordenamiento es fundamental tanto en matemáticas como en la resolución de problemas cotidianos. Además de los números ordinales, también se aplica en conceptos más avanzados, como la teoría de números y la combinatoria.
En resumen, el principio del ordenamiento en el contexto de los números ordinales es esencial para comprender cómo asignar posiciones específicas a elementos en una secuencia. Este concepto matemático es ampliamente aplicable en diversas disciplinas y situaciones cotidianas, y es fundamental para el desarrollo de habilidades de clasificación y organización tanto en matemáticas como en la vida real.
El principio de la cardinalidad es un concepto matemático fundamental que desempeña un papel crucial en la comprensión de los números ordinales. La cardinalidad se refiere a la habilidad de contar objetos en una colección o conjunto y determinar cuántos elementos hay en total. Este concepto es esencial como paso previo al entendimiento de los números ordinales.
La cardinalidad involucra el proceso de contar. Los estudiantes aprenden a contar objetos de uno en uno, asignando un número cardinal a cada objeto a medida que avanzan en la secuencia de conteo. Por ejemplo, contar del 1 al 10 implica asignar un número cardinal a cada número en esa secuencia: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
La cardinalidad permite determinar la cantidad total de objetos en un conjunto. Por ejemplo, al contar una colección de manzanas, la cardinalidad nos dice cuántas manzanas hay en total en esa colección.
La cardinalidad también permite comparar la cantidad de objetos en diferentes conjuntos. Los estudiantes pueden determinar cuál de dos conjuntos tiene más o menos objetos al contar y comparar sus números cardinales.
Antes de que los estudiantes puedan comprender y aplicar los números ordinales, deben tener una comprensión sólida de la cardinalidad. Los números ordinales se utilizan para describir la posición u orden de objetos en una secuencia, y esta secuencia se crea a través del proceso de conteo cardinal.
En resumen, la cardinalidad es el principio matemático que involucra la capacidad de contar objetos en una colección y determinar cuántos elementos hay en total. Es un concepto esencial para comprender los números ordinales, ya que los números ordinales se aplican a secuencias de elementos que se crean a través del proceso de conteo cardinal. El entendimiento sólido de la cardinalidad es un paso fundamental en el desarrollo de habilidades matemáticas y de resolución de problemas.

El principio de la correspondencia uno a uno es un concepto matemático fundamental que desempeña un papel crucial en la comprensión y aplicación de los números ordinales. Este principio establece que cada elemento en una secuencia se corresponde con un número ordinal único y, a su vez, cada número ordinal se corresponde con un elemento único en la secuencia. La correspondencia uno a uno asegura que no puede haber duplicados ni elementos faltantes en la secuencia.
Cada elemento en la secuencia tiene un número ordinal exclusivo que lo identifica. Por ejemplo, en una fila de estudiantes, el estudiante en la posición tercera tiene una correspondencia única con el número ordinal "tercero".
La correspondencia es bidireccional. Esto significa que no solo cada elemento se corresponde con un número ordinal, sino que también cada número ordinal se corresponde con un elemento específico. En otras palabras, se puede identificar el elemento al conocer su número ordinal y viceversa.
No puede haber duplicados en la correspondencia uno a uno. Cada número ordinal debe ser único y asignado a un solo elemento en la secuencia. No puede haber dos elementos que se etiqueten como "primero", por ejemplo.
Todos los elementos en la secuencia deben tener una correspondencia numérica ordinal. No puede haber números ordinales que falten en la secuencia ni elementos que no estén etiquetados con un número ordinal.
En resumen, el principio de la correspondencia uno a uno es fundamental en la aplicación de números ordinales. Este principio matemático asegura que cada elemento en una secuencia se relacione de manera única con un número ordinal y viceversa, sin duplicados ni elementos faltantes. La correspondencia uno a uno es una base esencial para el entendimiento preciso y la aplicación efectiva de los números ordinales en una variedad de contextos matemáticos y prácticos.
El principio de la secuencia es un concepto matemático fundamental que desempeña un papel central en la comprensión y aplicación de los números ordinales. Los números ordinales están intrínsecamente relacionados con la idea de secuencia, lo que implica que los estudiantes deben ser capaces de reconocer y seguir una secuencia numérica ascendente (primero, segundo, tercero, etc.) y, en algunos casos, también una secuencia numérica descendente (décimo, noveno, octavo, etc.).
La secuencia numérica ascendente es aquella en la que los números ordinales aumentan a medida que avanzamos en la serie. Comienza con "primero" y avanza en orden hacia "segundo", "tercero" y así sucesivamente.
En algunos casos, también se requiere comprender la secuencia numérica descendente, que implica que los números ordinales disminuyen a medida que avanzamos en la serie. La secuencia numérica ordinal permite a los estudiantes identificar la posición o el lugar de un elemento en una serie ordenada. Por ejemplo, si alguien es el "quinto" en una fila, se encuentra en la posición número cinco en esa secuencia.
Los estudiantes deben ser capaces de recorrer la secuencia numérica ordinal de manera ordenada, reconociendo cada número ordinal y comprendiendo su lugar relativo en la serie.
La secuencia numérica ordinal también es reversible, lo que significa que los estudiantes deben poder avanzar y retroceder en la serie de números ordinales según sea necesario.
En resumen, el principio de la secuencia es esencial para la comprensión y aplicación de los números ordinales. Los estudiantes deben ser capaces de reconocer, seguir y manipular secuencias numéricas ordinales tanto ascendentes como descendentes para describir la posición de elementos en una serie ordenada. Este concepto matemático es fundamental para el desarrollo de habilidades de resolución de problemas y o rganización en una variedad de contextos.
El principio de la partición es un concepto matemático crucial que se relaciona con el uso efectivo de los números ordinales. La partición es fundamental para evitar errores como la doble contabilización o la omisión de elementos al asignar números ordinales. Implica que los estudiantes deben ser capaces de dividir los elementos en dos categorías distintas: aquellos que han sido contados y aquellos que aún no han sido contados.
La partición es esencial para evitar contar elementos más de una vez. Los estudiantes deben asegurarse de que cada elemento se coloque en la categoría correcta después de contar y asignar un número ordinal.
Del mismo modo, la partición evita la omisión de elementos. Cada elemento en el conjunto debe ser clasificado como "contado" o "no contado" para garantizar que ninguno quede fuera de la cuenta.
La partición ayuda a crear un proceso de conteo claro y organizado, lo que facilita la asignación precisa de números ordinales.
En resumen, el principio de la partición es fundamental para el uso efectivo de los números ordinales y el proceso de conteo en general. Los estudiantes deben ser capaces de separar elementos en dos categorías distintas: aquellos que han sido contados y aquellos que aún no han sido contados. Esto ayuda a evitar errores de conteo, garantiza la precisión en la asignación de números ordinales y sienta las bases para una comprensión sólida de los conceptos matemáticos relacionados con el orden y la secuencia.
El principio de la etiquetación es un concepto matemático esencial que se relaciona con el uso efectivo de los números ordinales. La etiquetación implica la capacidad de conocer la secuencia de los números ordinales (primero, segundo, tercero, etc.) y asignar el número correcto a cada elemento en la secuencia. Esto requiere que los estudiantes tengan un conocimiento sólido de la nomenclatura ordinal, es decir, el conjunto de palabras y términos utilizados para describir la posición o el orden de los elementos en una secuencia.
Para aplicar números ordinales de manera efectiva, los estudiantes deben tener un conocimiento claro y preciso de la secuencia numérica ordinal. Deben poder recitarla de manera ordenada: primero, segundo, tercero, cuarto, etc.
La etiquetación implica asignar el número ordinal correcto a cada elemento en una secuencia. Por ejemplo, si se cuenta una fila de estudiantes, el primer estudiante se etiqueta como "primero", el segundo como "segundo", y así sucesivamente.
La etiquetación requiere precisión. Cada número ordinal debe asignarse al elemento correcto en la secuencia, y no debe haber ambigüedad en la asignación.
En resumen, el principio de la etiquetación es esencial para la comprensión y aplicación efectiva de los números ordinales. Requiere que los estudiantes conozcan la secuencia numérica ordinal y asignen con precisión el número ordinal correcto a cada elemento en una secuencia. La etiquetación se basa en la nomenclatura ordinal y es relevante tanto en el desarrollo del lenguaje como en el de habilidades matemáticas, y se aplica en una variedad de contextos prácticos y matemáticos.
El principio de la generalización es un concepto matemático fundamental que se relaciona con la comprensión y aplicación de los números ordinales. A medida que los estudiantes avanzan en su comprensión de los números ordinales, deben poder generalizar su conocimiento para aplicarlo a diferentes contextos y situaciones. Esto implica reconocer que los números ordinales se pueden utilizar en una variedad de escenarios, como describir la posición de estudiantes en una fila, los pasos en una receta o los lugares en una competencia deportiva.
La generalización implica la transferencia de conocimiento. Los estudiantes deben ser capaces de aplicar su comprensión de los números ordinales en una variedad de situaciones más allá de aquellas en las que originalmente aprendieron el concepto.
Los estudiantes deben ser capaces de identificar diferentes contextos en los que los números ordinales son relevantes. Esto puede incluir situaciones cotidianas, académicas o prácticas.
La generalización requiere flexibilidad conceptual. Los estudiantes deben comprender que los números ordinales pueden utilizarse de manera versátil para describir el orden o la posición de elementos en cualquier secuencia ordenada.
En resumen, el principio de la generalización es fundamental para la comprensión y aplicación efectiva de los números ordinales. Los estudiantes deben ser capaces de transferir su conocimiento de números ordinales a una variedad de situaciones y contextos, reconociendo que estos números pueden utilizarse para describir el orden o la posición en una amplia gama de secuencias ordenadas. La generalización es esencial para el desarrollo de habilidades matemáticas y de pensamiento crítico.
En conclusión, los principios fundamentales que sustentan la comprensión de los números ordinales, como el ordenamiento, la cardinalidad, la correspondencia uno a uno, la secuencia, la partición, la etiquetación y la generalización, son pilares esenciales en el desarrollo de habilidades matemáticas y cognitivas. Estos principios no solo proporcionan una base sólida para la aplicación precisa de números ordinales, sino que también fomentan la organización, el razonamiento y la resolución efectiva de problemas en diversos contextos, desde simples secuencias numéricas hasta situaciones prácticas y cotidianas. Así, la comprensión profunda de estos principios contribuye significativamente al desarrollo integral de habilidades matemáticas y al pensamiento crítico.
¡Gracias por leer!
Originalmente publicado 04/09/2023
Última actualización 04/09/2023
Últimas Entradas relacionadas: