

07/06/2023 (última actualización: 06/06/2023)
Aritmética
Contar
Infantil
Matemáticas
Teoría
Soroban
El aprendizaje de contar hasta 3 es un paso fundamental en el desarrollo del conocimiento matemático básico. Este proceso implica adquirir habilidades cognitivas y conceptuales, como comprender el concepto de cantidad, reconocer la secuencia numérica y comprender el Principio de Conservación. Es crucial tener en cuenta que el entendimiento sólido del concepto de cantidad sienta las bases para el aprendizaje matemático futuro.
Este artículo explora la importancia de comprender la cantidad, el orden y la secuencia en el proceso de contar hasta 3. Además, se aborda la necesidad de reflexionar sobre experiencias concretas para adquirir conceptos abstractos como el número y la conservación. Se destaca la importancia de brindar apoyo y tiempo suficiente para que los estudiantes desarrollen una comprensión sólida de la cantidad. El artículo también proporciona una descripción de cómo se puede abordar el aprendizaje de contar hasta 3 y ofrece juegos interactivo para fortalecer las habilidades matemáticas.
Este contenido se vincula con el
Nivel 1
de la materia ![]() y es pertinente al curso
y es pertinente al curso ![]()
Aprender a contar hasta 3 es un proceso fundamental en el desarrollo del conocimiento matemático básico. La habilidad para contar constituye la base para comprender y manipular cantidades, así como para realizar operaciones matemáticas más complejas en etapas posteriores.
El aprendizaje de contar hasta 3 implica adquirir una serie de habilidades cognitivas y conceptuales. En primer lugar, se debe comprender el concepto de cantidad y asociarlo con una representación numérica. Esto implica reconocer que el número 3 representa una cantidad específica de elementos o unidades.
Además, aprender a contar hasta 3 implica comprender el orden y la secuencia de los números. El alumnado debe ser capaz de recitar los números en el orden correcto, comprendiendo que el número siguiente en la secuencia es siempre uno más que el anterior. Esta habilidad de secuenciación es esencial para establecer las bases de la numeración.
Es importante tener en cuenta que el aprendizaje de contar hasta 3 es solo el comienzo de un proceso más amplio de desarrollo matemático. A medida que se adquieren habilidades numéricas más avanzadas, como contar hasta números más altos y comprender los conceptos de adición y sustracción, se construirá una base sólida para el aprendizaje de las matemáticas en etapas posteriores.
Es necesario comprender que en ausencia de un entendimiento sólido del concepto de cantidad, los estudiantes pueden tener la capacidad de contar los elementos, pero carecerán de comprensión del proceso subyacente. Por ejemplo, podrían ser capaces de contar dos conjuntos de objetos, pero no ser capaces de determinar cuál conjunto tiene más elementos cuando se les presenta esta pregunta. Esta limitación se debe a una falta de claridad en el concepto de cantidad, a pesar de su habilidad para asociar elementos individualmente y su conocimiento de la secuencia numérica y su representación simbólica. Este desafío radica en la necesidad de comprender también el Principio de Conservación.
Este principio establece que cuando dos conjuntos tienen la misma cantidad de elementos, esa igualdad se mantiene independientemente de cómo se coloquen los elementos dentro de cada conjunto. En otras palabras, la disposición o posición de los elementos no altera la cantidad total. Si dos conjuntos inicialmente tienen la misma cantidad de elementos, seguirán teniendo la misma cantidad sin importar cómo se distribuyan o se organicen en cada conjunto.
La adquisición de conceptos abstractos, como el número y la conservación, se logra a través de la reflexión sobre experiencias concretas. El desarrollo de la noción de número comienza al observar conjuntos físicos y, de manera progresiva, se van identificando equivalencias y relaciones lógicas que forman la idea de que los números representan una cualidad, específicamente la cantidad, de un grupo de objetos. Aunque los números en sí mismos no pueden ser tocados, se comprende que son entidades abstractas que existen independientemente de la posición o el tamaño de los elementos. Es necesario que los estudiantes interioricen en su pensamiento la noción de que un número es una cualidad abstracta que trasciende las características físicas de los objetos.
Uno de los desafíos más recurrentes al interactuar con personas que expresan aversión hacia las matemáticas es que no tuvieron suficiente oportunidad para desarrollar una comprensión profunda del concepto de cantidad. Como resultado, se enfrentan a dificultades para comprender el propósito y significado de las operaciones matemáticas, y perciben las matemáticas como una materia en la cual deben memorizar reglas y procedimientos carentes de sentido. Sin embargo, es importante destacar que las matemáticas se centran en descubrir y comprender las relaciones que existen entre las diferentes entidades y fenómenos. Más allá de la mera memorización, las matemáticas nos brindan la capacidad de explorar y establecer conexiones entre conceptos, lo cual constituye su verdadera esencia.
Por lo tanto, si identificas que un estudiante aún no ha adquirido plenamente el concepto de cantidad, es fundamental no pasarlo por alto. No importa si el estudiante logra aprobar los exámenes momentáneamente; hasta que no logre comprender el concepto por sí mismo, no podrá darle sentido a conceptos más complejos. Es esencial brindarle el tiempo y el apoyo necesario para que desarrolle una comprensión sólida de la cantidad, ya que constituye un cimiento fundamental para abordar de manera significativa aspectos matemáticos más avanzados.
Una vez que se ha presentado la fundamentación teórica relacionada con el proceso de contar y el concepto de cantidad, daremos inicio al aprendizaje de contar hasta 3.
En primer lugar, se inicia el proceso de aprendizaje mediante la verbalización de los números, es decir, se aprende a pronunciar correctamente las palabras correspondientes a cada número: "uno", "dos" y "tres". En esta etapa inicial, es común utilizar recursos visuales como los dedos para contar y reforzar la asociación entre las palabras y la cantidad representada. Posteriormente, se introduce la correspondencia entre dichas palabras y sus símbolos numéricos: 1, 2 y 3. En el caso particular de un contexto educativo con personas adultas, se parte de la premisa de que ya tienen conocimiento previo de los números y su representación simbólica.
En el proceso de aprendizaje, se introducen los símbolos numéricos y su correspondencia con la cantidad de elementos de un conjunto que utilizaremos como referencia. En nuestro caso, nos enfocaremos en los siguientes símbolos y su respectiva representación:
Veamos su representación en la siguiente imagen:
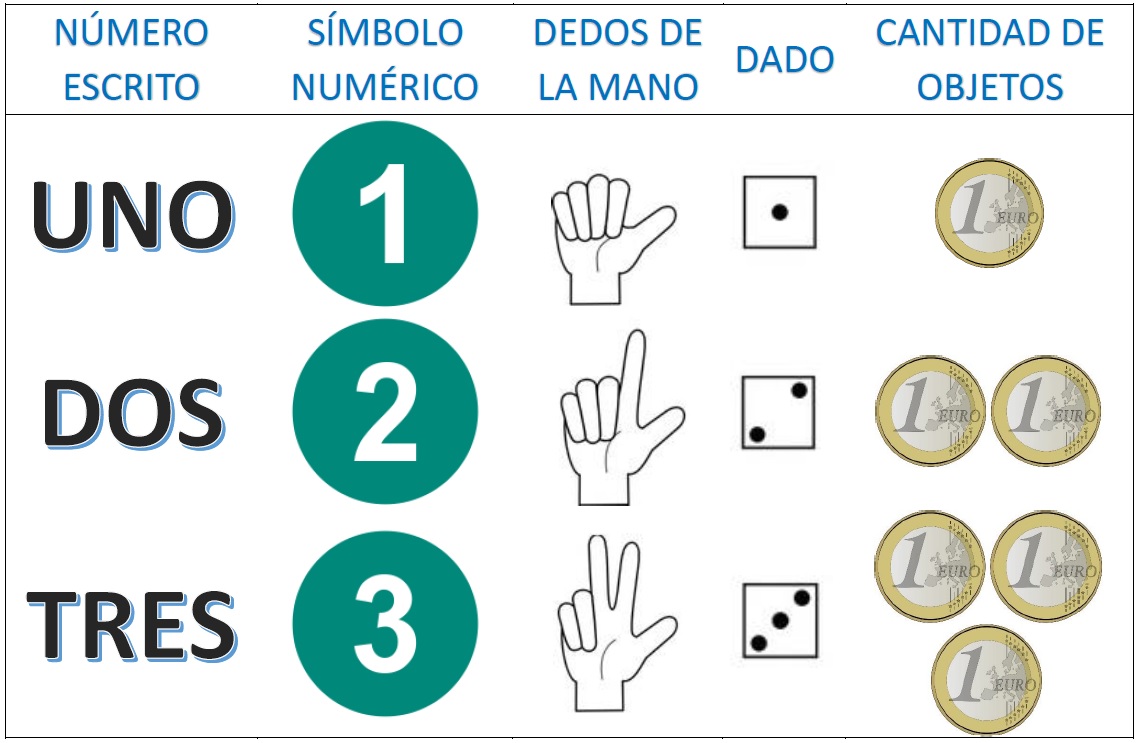
En el caso de utilizar un soroban (recomendado sobre el ábaco), su funcionamiento se basa en una representación decimal similar al ábaco tradicional. Cada columna del soroban corresponde a una posición de valor, como unidades, decenas, y así sucesivamente. Sin embargo, en comparación con el ábaco tradicional, existen dos diferencias fundamentales.
En primer lugar, no todas las cuentas del soroban tienen el mismo valor. Las cuentas inferiores tienen un valor de 1 cada una, mientras que las cuentas superiores representan un valor de 5. Esta distinción en los valores asignados a las cuentas es una característica distintiva del soroban.
Además, a diferencia del ábaco tradicional, todas las cuentas del soroban están siempre visibles y adquieren valor a medida que se acercan a la barra central, perdiendo valor a medida que se alejan de ella. Este aspecto dinámico del soroban permite una representación visual más clara de los cálculos y facilita el seguimiento de los valores numéricos en cada columna.

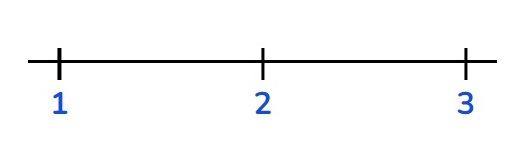
Una técnica eficaz para introducir a los niños pequeños en el mundo de las matemáticas es a través de la recta numérica. Aunque los niños de edad preescolar pueden no estar listos para escribir o dibujar números con precisión, es fundamental que comiencen a entender cómo se representan y se ubican estos números en una recta numérica. Esta comprensión temprana ayuda a desarrollar una base sólida para conceptos matemáticos más avanzados.
Para enseñar la recta numérica, los docentes pueden utilizar herramientas visuales y prácticas, como una recta numérica grande en el aula, marcadores de posición, o incluso una cuerda en el suelo. Lo importante es que los niños puedan visualizar y, si es posible, interactuar físicamente con la recta numérica. Colocar los números del 1 al 3 en la recta numérica ayuda a los niños a comprender que cada número tiene una posición única y que el espacio entre cada número es constante. Esto establece una comprensión temprana de la secuencia y el espaciado de los números.
Una actividad sugerida es pedir a los niños que coloquen objetos o etiquetas en las posiciones correctas del 1 al 3 en la recta numérica. Durante esta actividad, es esencial que el docente guíe y explique la relación entre cada número y su posición. A través de esta interacción táctil y visual, los niños no solo aprenden a identificar los números, sino también a comprender su relación espacial y secuencial, lo cual es un paso crucial en el desarrollo de habilidades matemáticas básicas.
En resumen, el proceso de aprender a contar hasta 3 en el contexto de la educación infantil es fundamental para establecer las bases del conocimiento matemático. Implica comprender el concepto de cantidad, la secuencia de números y el principio de conservación. La comprensión sólida de la cantidad es esencial para abordar conceptos matemáticos más avanzados en el futuro. Además, es crucial ofrecer apoyo y tiempo a aquellos estudiantes que aún no han adquirido plenamente este concepto, ya que constituye un cimiento fundamental para su desarrollo matemático. Se pueden utilizar símbolos numéricos y herramientas visuales como el soroban para facilitar el proceso de aprendizaje y la comprensión de las relaciones numéricas.
Este enfoque pedagógico contribuirá al desarrollo de habilidades matemáticas sólidas en los estudiantes, permitiéndoles explorar y establecer conexiones entre conceptos y comprender la esencia de las matemáticas más allá de la memorización de reglas y procedimientos.
¡Gracias por leer!
Originalmente publicado 07/06/2023
Última actualización 06/06/2023
Últimas Entradas relacionadas: